Table of Contents

@miloyip has published a post recently which motioned the Alias Method to generate a discrete random variable in O(1). After some research, I find out that it is a neat and clever algorithm. Following are some notes of my study on it.

What is Alias Method

Alias method is an efficient algorithm to generate a discrete random variable with specified probability mass function using a uniformly distributed random variable.

Let $Z$ be the discrete random variable which has n possible outcomes $z_0,z_1,\ldots,z_{n-1}$. To make the discussion below simple, we study another variable $Y$, where $P\{Y=i\}=P\{Z=z_i\}$. And when $Y$ takes on value $i$, let $Z$ be $z_i$. So $Z$ can be generated from $Y$.

Random variable $X$ is uniformly distributed in $(0, n)$, which probability density function is

\[
    f(x) = \left\{
     \begin{array}{rl}
      1/n & \text{if } 0 < x < n\\
      0 & \text{otherwise}\\
     \end{array} \right.
\]

Now generate a variable $Y'$ that

\[
    Y' =  \left\{
     \begin{array}{rl}
      \lfloor x  \rfloor & \text{if } (x - \lfloor x \rfloor) < F(\lfloor x \rfloor)\\
      A(\lfloor x \rfloor)  & \text{otherwise}\\
     \end{array} \right.
\]

$A(i)$ is the alias function. When $x$ falls in range $[i, i + 1)$ ($i$ is an integer), $y$ has the probability $F(i)$ to be $i$, and probability $1 - F(i)$ to be $A(i)$. Because $x$ is uniformly distributed,

\[
    \begin{aligned}
    P\{x \in [i, i + F(i))\}     &= \displaystyle\int_i^{i+F(i)}\frac{1}{n}dx\\
                             &= (i + F(i) - i) \times 1/n\\
                             &= F(i)/n,\\
                             \\
    P\{x \in [i + F(i), i + 1)\} &= \displaystyle\int_{i+F(i)}^{i+1}\frac{1}{n}dx\\
                             &= (i + 1 - (i + F(i))) \times 1/n\\
                             &= (1-F(i))/n
    \end{aligned}
\]

Let’s denote the set of values $j$ that satisfies $A(j) = i$ as $A^{-1}(i)$. The generated variable $Y'$ has following probability mass function:

\[
    P\{Y' = i\} = F(i)/n + \sum_{j \in A^{-1}(i)}\frac{1-F(j)}{n}
\]

Alias method is the algorithm to construct $A$ and $F$ so that $P\{Y' = i\}$ equals to $P\{Y = i\}$ for all $i$. Because the domain of both $A$ and $F$ are integers $0,1,\ldots,n-1$, they can be stored in array and values can be looked up in O(1), where the space efficiency is in O(n).

In miloyip’s implementation, $A$ and $F$ are stored in std::vector<AliasItem> mAliasTable, where $A$’s values are stored in AliasItem::index and $F$’s values are AliasItem::prob.

Algorithm

Construct Steps

Initialize the set $S$ to be ${0,1,\ldots,n-1}$ and n variables $p_i$ that with values:

\[ p_i = P\{Y=i\}, i \in S \]

Denote the number of elements in $S$ as $\|S\|$. We have a important invariant that

\[ \sum_{i \in S}{p_i} = \|S\| / n \]

At the beginning of the algorithm, the invariant holds because the sum of all probabilities must equal to 1.

The algorithm is performed using following steps.

  1. If there is an element $i$ in set $S$ such that $p_i < 1/n$, there must be a $j$ in set $S$ such that $p_j > 1/n$.1 Let $A(i) = j$ and $F(i) = p_i / (1/n) = p_i \times n$. Remove $i$ from $S$ and subtract $n/1 - p_i$ from $p_j$. It is easy to verify that the invariant still holds after these changes.2
  2. Repeat step 1 until $S$ is empty or there is no more elements $i$ in $S$ that $p_i < 1/n$. If $S$ is empty, the algorithm finishes. Otherwise for all remaining $i$ in $S$, we must have $p_i = 1/n$.3 Let $A(i)=i$ and $F(i)=p_i\times n=1$ for all remaining $i$, and remove them from the set $S$.

The algorithm finishes when $S$ becomes empty, and an element is removed only when its corresponding $A$ and $F$ has been determined, so all values of $A$ and $F$ has been generated.

In miloyip’s implementation, $p_i$ is stored in AliasItem::prob before $i$ is removed from the set. When $i$ is removed from the set, AliasItem::prob is set to $F(i)$.

Correctness

The invariant holds at the beginning and at the end of each step, it guarantees that the algorithm can finish. It is easy to prove it using mathematical induction. So we only need to prove $P\{Y'=i\}=P\{Y=i\}$ for any $i$, i.e.,

\[ P\{Y = i\} = F(i)/n + \sum_{j \in A^{-1}(i)}\frac{1-F(j)}{n} \]

Denote $p'_i$ as the value of $p_i$ when $i$ is removed from set $S$. Check the construction steps again, we get following properties:

  1. No $p_i$ can increase. Thus $p_i <= P\{Y=i\}$ in all steps and $p'_i <= P\{X=i\}$.
  2. $p_i$ decreases only when its initial value $P\{Y=i\}>1/n$. So if $P\{Y=i\}<=1/n$, $p_i = P\{Y=i\}$ throughout the algorithm and $p'_i=P\{Y=i\}$.
  3. $F(i) = p'_i \times n$
  4. $i$ is removed only when $p_i \leq 1/n$, i.e., $p'_i \leq 1/n$, thus $F(i)=p'_i \times n \leq 1$.
  5. $A(j)$ is set to a value $i \neq j$ only if $p_i > 1/n$ (see step 1), i.e., $P\{Y=i\}>1/n$.

Now consider value $i$ when $P\{Y=i\}<1/n$, $P\{Y=i\}=1/n$ and $P\{Y=i\}>1/n$.

P{Y=i} < 1/n

If $P\{Y=i\} < 1/n$, from property 2 and property 3, $F(i) = p'_i \times n = P\{Y=i\} \times n$.

Apparently $A^{-1}(i) = {}$, because $A$ is either set to value $j$ where $p_j>1/n$ in step 1 or $k$ where $p_k = 1/n$ in step 2.

Thus

\[
\begin{aligned}
 &F(i)/n + \sum_{j \in A^{-1}(i)}\frac{1-F(j)}{n}\\
=&F(i)/n\\
=&P\{Y=i\} \times n / n\\
=&P\{Y=i\}
\end{aligned}
\]

which completes the proof.

P{Y=i} = 1/n

If $P\{Y=i\} = 1/n$, apparently $A(i) = i$. If there’s another value $j\neq~i$ also satisfies $A(j) = i$, from property 4, $P\{Y=i\} > 1/n$, conflict with the condition. So $A^{-1}(i) = {i}$

Thus

\[ \begin{aligned}
 &F(i)/n + \sum_{j \in A^{-1}(i)}\frac{1-F(j)}{n}\\
=&F(i)/n + (1-F(i))/n\\
=&1/n
\end{aligned} \]

which completes the proof.

P{Y=i} > 1/n

When $P\{Y=i\} > 1/n$, apparently i is not in $A^{-1}(i)$.

Consider each value $j$ in set $A^{-1}(i)$. Once $j$ is removed from $S$, $A(j)$ is set to $i$ and $1/n - p'_j$ is subtracted from $p_i$. Thus

\[ p'_i = P\{Y=i\} - \sum_{j \in A^{-1}(i)}(1/n - p'_j) \]

Then

\[ \begin{aligned}
 &F(i)/n + \sum_{j \in A^{-1}(i)}\frac{1-F(j)}{n}\\
=&p'_i \times n / n + \sum_{j \in A^{-1}(i)}\frac{1-(p'_j \times~n)}{n}\\
=&P\{Y=i\} - \sum_{j \in A^{-1}(i)}(1/n - p'_j)\ + \sum_{j \in A^{-1}(i)}(1/n - p'_j)\\
=&P\{Y=i\}
\end{aligned} \]

For all $i$, $P\{Y'=i\} = P\{Y=i\}$, the proof completes.

Intuitive Presentation

The algorithm can be presented in intuitive meaning. The range $(0, n]$ is split into n consecutive sub ranges $(i, i + 1]$ for $i = 0, 1, \ldots, n - 1$. The probability of $X$ falls into any range is $(i + 1 - i) \times 1/n = 1/n$.

For $P\{Y=i\} = 1/n$, we can allocate the whole slot $i$ to it. Let $Y=i$ when $x$ falls in $(i, i + 1]$ which has the probability $1/n$.

If $P\{Y=i\} < 1/n$, we can allocate the starting part $(i,i+n\times~P\{Y=i\}]$ in $(i,i+1]$. Let $Y = i$ when $x$ falls in $(i, i + n\times P\{Y=i\}]$, where the probability is $n\times~P\{Y=i\}\times(1/n)=P\{Y=i\}$.

If $P\{Y=i\} > 1/n$, we can allocate unused ranges in $(j + n\times P\{Y=j\}, j + 1]$ for any $j$ that $P\{Y=j\} < 1/n$. However, unused range is not allowed to be split again.

See the figure below, which demonstrates how to generate $Y$ with probability mass function $n = 5$

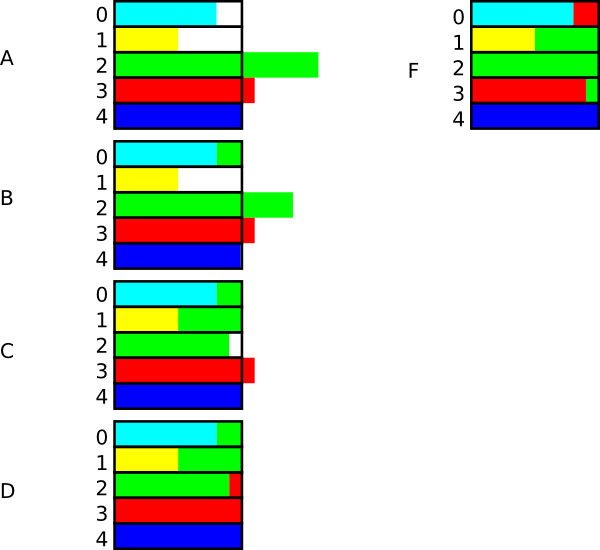
Alias Method
Alias Method
  • $P\{Y=0\} = 0.16$
  • $P\{Y=1\} = 0.1$
  • $P\{Y=2\} = 0.32$
  • $P\{Y=3\} = 0.22$
  • $P\{Y=4\} = 0.2$

$P\{Y=4\}=1/n$, so let $Y = 4$ only when $x$ falls in $(4, 5]$, which probability is $(5-4)\times 0.2 = 0.2$.

$P\{Y=0\}=0.16<0.2$, so let $Y = 0$ only when $x$ falls in $(0,0.16\times~5]$, i.e., $(0,0.8]$, which probability is $(0.8-0)\times~0.2=0.16$. $(0.8,1]$ is unused.

$P\{Y=1\}$ is the same. $(1,1.5]$ is allocated and $(1.5,2]$ is unused.

$P\{Y=2\} = 0.32 > 0.2$, it needs ranges with total length $0.32\times~5=1.6$. We allocate the range $(0.8, 1]$ and $(1.5, 2]$. The remaining length $1.6-0.2-0.5=0.9<1$, then we can allocate a part of its own slot. Finally, three ranges have been allocated, $(0.8,1]$, $(1.5,2]$ and $(2,2.9]$. $(2.9,3]$ is unused.

Follow the same step to handle $Y=3$. The final allocation is depicted in $D$. The allocation is not unique, $F$ depicts another solution.

References

  1. If all $j$ except $i$ that $p_j \leq 1/n$, Sum up both end of the inequalities for all $j$ and $p_i < 1/n$, we can get $\sum_{i \in S}{p_i} < \|S\| / n$ which is conflict with the invariant. ↩︎

  2. The right side has decreased $1/n$ because $\|S\|$ has decreased 1. The left side has decreased $p_i + (n/1 - p_i) = 1/n$, because $i$ is removed from the set and $(n/1 - p_i)$ is subtracted from $p_j$. Thus both side decrease the same amount, the equality still holds. ↩︎

  3. Because no $p_i < 1/n$, then $p_i \geq 1/n$. To satisfy the invariant, no $p_i$ can be larger then $1/n$. Thus for all $i$ in $S$, $p_i = 1/n$. ↩︎